CNN---LeNet5

Posted on

深度学习之CNN，学习网络结构，了解代码实现。卷积神经网络的知识点包括：局部感知、参数共享、池化。

用于图像分类的CNN经典网络有：LeNet5、AlexNet、VGG、GoogleNet、ResNet等，今天我们主要学一下LeNet5结构。

Html语法在Markdown中段落首行缩进的功能，还不错！

理解卷积神经网络，需要先知道的几个概念。

  1. 局部感知

    • 每个神经元对图像的局部进行感知，然后在更高层将局部信息综合起来得到全局信息。

  2. 参数共享

    • 局部连接中隐藏层的每个神经元连接的是一个10×10的局部图像，因此有10×10个权值参数，将这10×10的权值参数共享给剩下的神经元。

    • 可以有效的减少训练参数，加速训练过程。

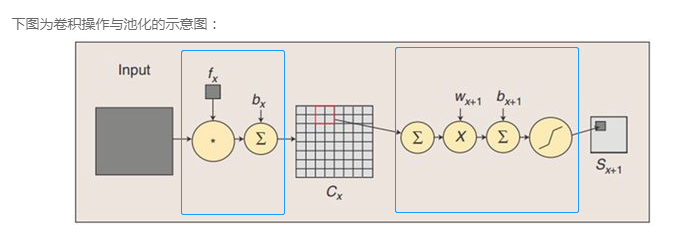
    • 卷积操作又包含以下：

      • 单核单通道卷积

        • 通过一个卷积核对一张图像进行卷积，生成一张feature map.

      • 多核单通道卷积

        • 一个卷积核提取的特征不充分。

        • k个10×10卷积核，对应训练参数为k×10×10(不包含偏置参数).

        • 卷积的过程就是特征提取的过程。

        • 假设对一个1000×1000的图像用k个卷积核10×10做卷积，stride为1，则隐层的节点数量为：k×（1000-100+1）×（1000-100+1）.

      • 多核多通道卷积

        • 多通道卷积操作通常作用在RGB或者ARGB(A代表透明度)的图像上。
        • 对于堆叠卷积层，pooling层之后可以继续接一个卷积层。对池化层的多个Feature Map操作即为多通道卷积。
        • 多核说的是卷积核个数，多通道说的是卷积核层数。
        • 假设对于ARGB图像，用2个卷积核进行卷积操作。每个卷积核会对应4个卷积模版（各不相同），卷积的Feature Map对应的位置的值是4个卷积模版分别作用在4个通道对应位置处的卷积结果相加然后取激活函数得到的。所以参数的数目为4×2×卷积核的长×卷积核的宽。

  3. 池化

    • 对卷积后的Feature Map进行池化操作。包括:最大池化，平均池化。

此处疑问：为什么卷积和池化层能起到作用？参考

深度学习正是通过卷积操作实现从细节到抽象的过程。因为卷积的目的就是为了从输入图像中提取特征，并保留像素间的空间关系。何以理解这句话？我们输入的图像其实就是一些纹理，此时，可以将卷积核的参数也理解为纹理，我们目的是使得卷积核的纹理和图像相应位置的纹理尽可能一致。当把图像数据和卷积核的数值放在高维空间中，纹理等价于向量，卷积操作等价于向量的相乘，相乘的结果越大，说明两个向量方向越近，也即卷积核的纹理就更贴近于图像的纹理。因此，卷积后的新图像在具有卷积核纹理的区域信号会更强，其他区域则会较弱。这样，就可以实现从细节（像素点）抽象成更好区分的新特征（纹理）。每一层的卷积都会得到比上一次卷积更易区分的新特征。

而池化目的主要就是为了减少权重参数，但为什么可以以Maxpooling或者MeanPooling代表这个区域的特征呢？这样不会有可能损失了一些重要特征吗？这是因为图像数据在连续区域具有相关性，一般局部区域的像素值差别不大。比如眼睛的局部区域的像素点的值差别并不大，故我们使用Maxpooling或者MeanPooling并不会损失很多特征。

接下来，LeNet网络的结构：

输入层-c1卷积层-s2池化层-c3卷积层-s4池化层-c5卷积层-F6全连接层-输出层

LeNet

–输入层–

​ 1 张32×32的图片

–C1卷积层–
  • 单通道，6个卷积核，得到6个feature maps
  • 卷积核大小（kernal size）:5×5
  • 特征图大小（feature map size）:(32-5+1)×(32-5+1)=28×28
  • 参数（parameters）：6×（5×5+1） 5×5为卷积核模版参数，1为骗纸偏置参数
  • 连接（connections）:6×（5×5 +1）×28×28
–S2池化层–
  • 6个池化核，得到6个feature maps
  • kernal size: 2×2
  • feature map size: (28/2)×(28/2)=14×14
  • parameters:6×(1+1)
  • parameters计算过程：2 ×2单元里的值相加然后再乘以训练参数w, 最后加上一个偏置参数b(feature map共享相同的w和b) (跟卷积不太一样这块，之前都是按卷积操作理解的，6 ×(4+1))
  • connections:6×（2×2+1）×14×14
  • 卷积操作与池化操作
–C3卷积层–
  • 多核多通道卷积：14个通道，16个卷积核，得到16个feature maps
  • kernel size:5×5
  • feature map size:(14-5+1)×(14-5+1)=10×10
  • parameters:6×（3×5×5+1）+6×（4×5×5+1）+3×(4×5×5+1)+1×(6×5×5+1)
  • S2与C3之间不是全连接而是部分连接
  • connections:6×（3×5×5+1）+6×（4×5×5+1）+3×（4×5×5+1）+1×（6×5×5+1）×10×10

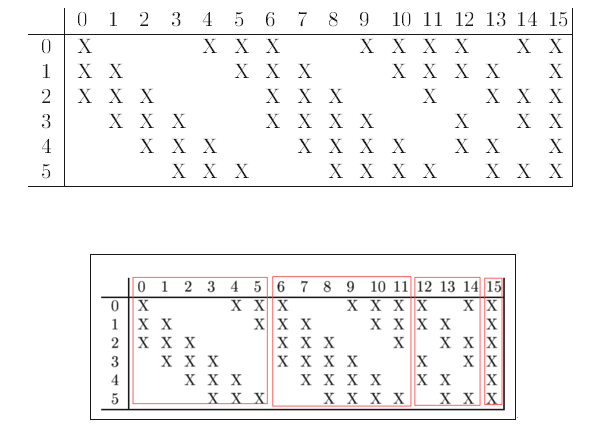
S2与C3的连接

  • 此处采用部分连接（Dropout）:
    • 减少可计算参数
    • 打破对称性，这样就能得到输入的不同特征集合
    • 从第0个feature map描述计算过程：
      • 用一个卷积核(对应3个卷积模板，但仍称为一个卷积核，可以认为是三维卷积核)分别与S2层的3个feature maps进行卷积，然后将卷积的结果相加，再加上一个偏置，再搞个激活函数就可以得出对应的feature map了
–S4池化层–
  • 16个池化核，得到16个feature maps
  • kernal size:2×2
  • feature map size: (10/2)×(10/2)=5×5
  • parameters:16×（1+1）
  • connections:16×（2×2+1）×5×5
–C5卷积层–
  • 120个卷积核，得到120个feature maps
  • kernal size:5×5
  • 每个feature map的大小都与上一层S4的所有feature maps进行连接，这样一个卷积核就有16个卷积模版。
  • feature map size:(5-5+1)×（5-5+1）=1×1，这样刚好变成了全连接，但是我们不把他写成F5，因为这只是巧合。
  • parameters:120×(16×5×5+1)
  • connections:120×(16×5×5+1）×1×1
–F6全连接层–
  • parameters:84×（120×1×1+1）
  • connections:84×（120×1×1+1）×1×1
–输出层–

得到分类结果，例：结果为数字几

代码实现：

‘’’ Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import os
print(os.getcwd())  #显示当前路径
os.chdir("./data/")  #在引号中填入你想放代码和数据的路径

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets("MNIST_data",one_hot=True) #读取数据
sess=tf.InteractiveSession()

#权重初始化设置
def weight_variable(shape):
    initial=tf.truncated_normal(shape,stddev=0.1)
    return tf.Variable(initial)

#偏置bias初始化设置
def bias_variable(shape):
    initial=tf.constant(0.1,shape=shape)
    return tf.Variable(initial)

def conv2d(x,W):
    return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')
    #卷积strides=[首位默认认为1，平行步长=1，竖直步长=1，尾位默认为1]

def max_pool_2x2(x):
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
    #池化strides=[首位默认为1，平行步长=2，竖直步长=2，尾位默认为1]

#placeholder:等待输入数据，x为占位符，接受型号为float32的数据，输入格式为矩阵[None,784]
x=tf.placeholder(tf.float32,[None,784])

y_=tf.placeholder(tf.float32,[None,10])

x_image=tf.reshape(x,[-1,28,28,1]) #[batch=-1,height=28,width=28,in_channels=1]

#C1:卷积层
W_conv1=weight_variable([5,5,1,32])  #[5x5卷积核，in_channels=1,out_channels=32=卷积核的个数]
b_conv1=bias_variable([32])  #[32=卷积核个数=bias个数]
h_conv1=tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1)  #激活函数
h_pool1=max_pool_2x2(h_conv1)  #池化方式：max pool

#C2:卷积层
W_conv2=weight_variable([5,5,32,64])
b_conv2=bias_variable([64])
h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2)
h_pool2=max_pool_2x2(h_conv2)

W_fc1=weight_variable([7*7*64,1024])
b_fc1=bias_variable([1024])
h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64])
h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)

keep_prob=tf.placeholder(tf.float32)
h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob)

W_fc2=weight_variable([1024,10])
b_fc2=bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2)

#损失函数loss function:交叉熵cross_entropy
cross_entropy=tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y_conv),reduction_indices=[1]))

#优化方法：AdamOptimizer学习率：1e-4 交叉熵：最小化
train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

correct_prediction=tf.equal(tf.argmax(y_conv,1),tf.argmax(y_,1)) #tf.equal返回布尔值，tf.argmax(y_,1):数字1代表最大值
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

tf.global_variables_initializer().run()
for i in range(20000):
    batch=mnist.train.next_batch(50) #喂入训练集的数据
    if i % 1000==0:  #批量梯度下降，把1000改为1：随机梯度下降
        train_accuracy=accuracy.eval(feed_dict={x:batch[0],y_:batch[1],keep_prob:1.0}) # train accuracy: accuracy.eval
        print("step %d,training accuracy %g"%(i,train_accuracy))
    train_step.run(feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={x:mnist.test.images,y_:mnist.test.labels,keep_prob:1.0}))

‘’’

实验结果

step 0,training accuracy 0.12
step 1000,training accuracy 1
step 2000,training accuracy 0.98
step 3000,training accuracy 0.98
step 4000,training accuracy 0.94
step 5000,training accuracy 1
step 6000,training accuracy 1
step 7000,training accuracy 1
step 8000,training accuracy 1

….